[백준 JAVA] 11727번 풀이 - 2xn 타일링 2
by mini_min

생각의 방향
dp 문제라는 것을 알고 문제에 숨겨진 규칙을 찾아내려 애썼다. 이전에 (2xn 타일링) 문제는 그리지 않고 직접 경우의 수를 적어서 문제를 풀었다. 이번에는 직접 도형을 그려서 점화식을 찾으려고 했다.
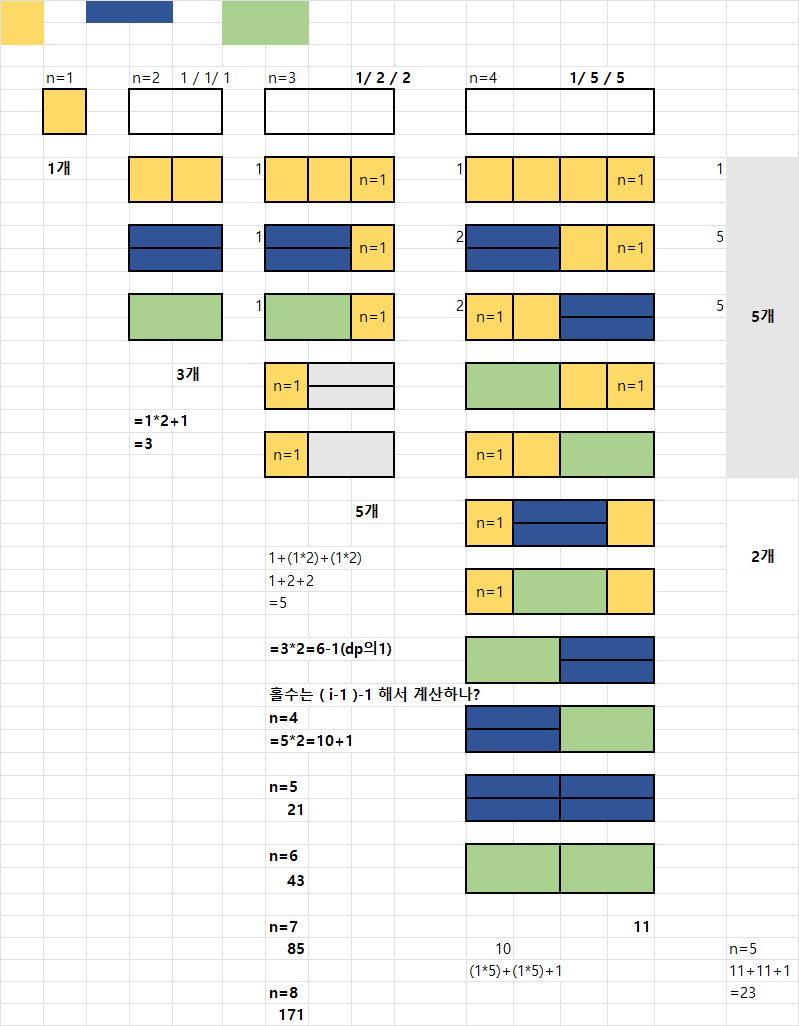
그런데, 그려도 모르겠는거다... dp 문제의 핵심은 이전에 계산한 값을 저장해뒀다가 사용하는 것이 핵심인데, 이전의 값이 어떻게 쓰이는건지 잘 보이지 않았다. 계속 시도해보고 다시 생각해서 결국 아래와 같은 점화식을 도출했다.
//n이 짝수인 경우
dp[i] = dp[i-1] * 2 + 1
//n이 홀수인 경우
dp[i] = dp[i-1] * 2 - 1
n이 짝수인 경우와 홀수인 경우, 이전 수열 값의 x2 + 1 값으로 원하는 답이 나오는 것을 알았다.
해당 점화식을 적용한 코드를 제출하여 문제를 맞췄다.
문제를 맞추고 다른 사람들은 어떻게 풀었나 구글링해보니, 많은 사람들은 아래와 같은 방법으로 풀었더라...! 문제는 맞췄지만, 아래 처럼 생각할 수 있구나를 배웠다.

코드
import java.util.Scanner;
/**
* 2xn 타일링 2
*
* 2*n 크기의 직사각형을 1*2, 2*1, 2*2 타일로 채우는 방법의 수를 구하시오.
* 첫째줄에 n이 주어진다.
* 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] dp = new int[1001];
//초기화!
dp[2] = 3;
dp[1] = 1;
//짝수는 이전 dp[i-1]*2 + 1 / 홀수는 이전 dp[i-1]*2 - 1
for(int i=3; i<=n; i++){
if(i%2==0){
dp[i] = (dp[i-1]*2 +1) % 10007;
} else if(i%2==1) {
dp[i] = (dp[i-1]*2 -1) % 10007;
}
}
System.out.println(dp[n]);
sc.close();
}
}
'매일매일 알고리즘 공부' 카테고리의 다른 글
| [백준 JAVA] 11052번 풀이 - 카드 구매하기 (+16194번) (0) | 2023.11.23 |
|---|---|
| [백준 JAVA] 9095번 풀이 - 1, 2, 3 더하기 (DP) (0) | 2023.11.21 |
| [백준 JAVA] 11726번 풀이 - 2xn 타일링 (0) | 2023.11.17 |
| [백준 JAVA] 17087번 풀이 - 숨바꼭질 6 (0) | 2023.11.15 |
| [백준 JAVA] 1676번 풀이 - 팩토리얼 0의 개수 (1) | 2023.11.14 |
블로그의 정보
개발자 미니민의 개발로그
mini_min