[알고리즘] 에라토스테네스의 체 란? (Prime 소수 구하기)
by mini_min
💡 👍🏻 [에라토스테네스의 체] 는 고대 그리스 수학자인 에라토스테네스가 만들어낸 소수를 판별하는 알고리즘이다. 마치 체를 가지고 수를 걸러내는 것 같아, '에라토스테네스의 채' 라고 부른다.
- 소수란 약수가 오로지 1인 수이다. 즉, 1을 제외한 수의 배수가 되는 수는 소수가 아니다.
- 소수를 대량으로 빠르고 정확하게 구할 때 이용한다.
- 지워지지 않은 수들이 소수이다.
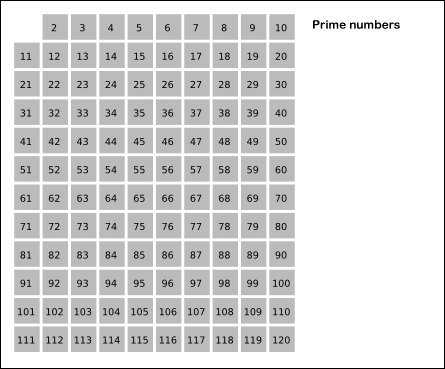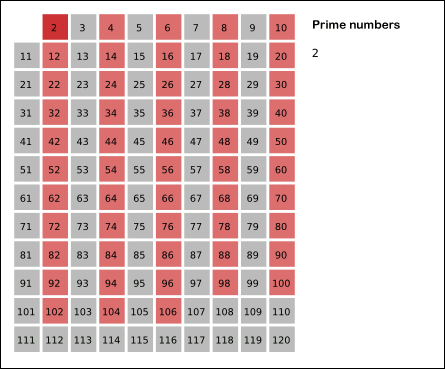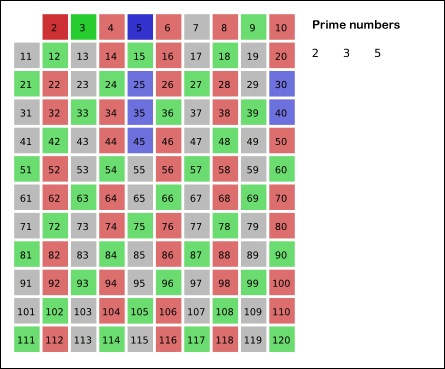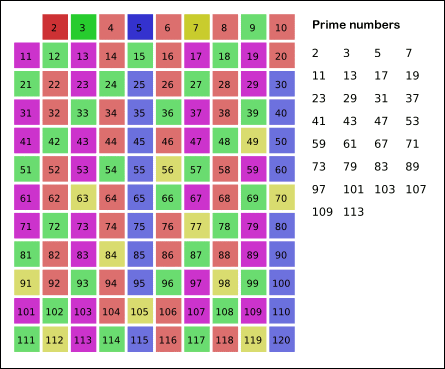
에라토스테네스의 원리
- 소수를 판별할 범위만큼 배열을 할당하여, 해당하는 값을 넣어주고 이후 하나 씩 지워가는 방법을 이용한다.
- 2부터 시작해서 특정 수의 배수에 해당되는 수를 모두 지운다.
- 2부터 시작해서 남은 수를 모두 출력한다.
🛠 예를 들어, 2부터 n까지의 수 중에서 소수를 구한다고 했을 때, 2는 소수니까 그대로 두고, n까지 순차적으로 2의 배수는 모두 제거한다. 다음으로 3도 소수이므로 그대로 두고, n까지 순차적으로 3의 배수를 제거한다. 4는 2의 배수라 제거되었기에 넘어간다. 5는 소수니까 그대로 두고, n까지 순차적으로 5의 배수를 제거한다.
이 과정을 n의 제곱근까지 반복한다. (for int i = 0; i ≤ sqrt(n); i++) …
n의 제곱근까지만 반복하는 이유
n의 제곱근 이상의 숫자를 제곱해봤자, 어차피 n보다 큰 값이 나오므로 더 이상의 연산은 의미가 없다.
ex) 16까지 수 중에 소수를 모두 구하고 싶을 때,
16의 제곱근은 4… 4보다 큰 숫자 5의 제곱은 25이므로 범위를 벗어나서 의미가 없어진다.
예제
- n까지의 범위에서 소수를 구하고자 하면, n크기의 배열을 만든다.
- n의 제곱근까지의 수(2~4)의 배수를 모두 지운다.
package quiz;
public class eratos {
public static void main(String[] args) throws Exception {
//16까지의 수 중에서 소수를 구하고 싶을 때.
//1. 배열 만들기
int[] arr = new int[16+1];
for ( int i = 2; i <= 16; i++ ){
arr[i] = i;
}
for ( int i = 2; i <= Math.sqrt(16); i++ ) {
if (arr[i] == 0) {
continue;
}
//특정 수의 배수 지우기.
for ( int j = i + i; j <= 16; j += i){
arr[j] = 0;
}
}
for (int i = 0; i <= 16; i++) {
if (arr[i] != 0) {
System.out.println(arr[i]);
}
}
}
}
'매일매일 알고리즘 공부 > 알고리즘 개념' 카테고리의 다른 글
| [자료구조] 원형 큐(Circular Queue) 개념 (0) | 2023.10.23 |
|---|---|
| [알고리즘] 좌표 압축 개념 (대소 관계로 정렬) (1) | 2023.10.16 |
| [알고리즘] 유클리드 호제법 (GCD) (0) | 2023.08.29 |
| [알고리즘] 상한가, 하한가 구하기 (이진 탐색 활용) (0) | 2023.08.21 |
| [알고리즘] 계수 정렬 (Counting sort) 개념 + 백준 10989번 예제 (0) | 2023.08.17 |
블로그의 정보
개발자 미니민의 개발로그
mini_min